친구, 우리 주변의 모든 것이 단지… 홀로그램이라면?
문제는 그럴 수 있다는 것입니다. 미시간 대학교의 물리학자가 사용합니다.[{” attribute=””>quantum computing and machine learning to better understand the idea, called holographic duality.
Holographic duality is a mathematical conjecture that connects theories of particles and their interactions with the theory of gravity. This conjecture suggests that the theory of gravity and the theory of particles are mathematically equivalent: what happens mathematically in the theory of gravity happens in the theory of particles, and vice versa.
Both theories describe different dimensions, but the number of dimensions they describe differs by one. So inside the shape of a black hole, for example, gravity exists in three dimensions while a particle theory exists in two dimensions, on its surface—a flat disk.
To envision this, think again of the black hole, which warps space-time because of its immense mass. The gravity of the black hole, which exists in three dimensions, connects mathematically to the particles dancing above it, in two dimensions. Therefore, a black hole exists in a three dimensional space, but we see it as projected through particles.
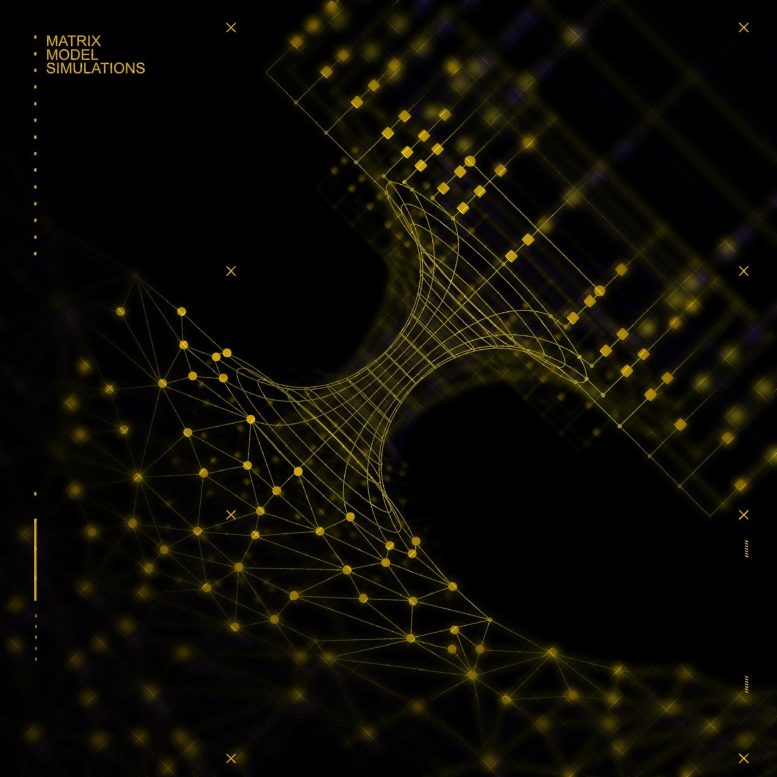
Enrico Rinaldi, research scientist in the University of Michigan Department of Physics, is using two simulation methods to solve quantum matrix models which can describe what the gravity of a black hole looks like. In this image, a pictorial representation of curved space time connects the two simulation methods. On the bottom, a deep learning method is represented by graphs of points (neural network), while the quantum circuit method on top is represented by lines, squares and circles (qubits and gates). The simulation methods merge with each side of the curved space time to represent the fact that gravity properties come out of the simulations. Rinaldi is based in Tokyo and hosted by the Theoretical Quantum Physics Laboratory at the Cluster for Pioneering Research at RIKEN, Wako. Credit: Enrico Rinaldi/U-M, RIKEN and A. Silvestri
Some scientists theorize our entire universe is a holographic projection of particles, and this could lead to a consistent quantum theory of gravity.
“In Einstein’s General Relativity theory, there are no particles—there’s just space-time. And in the Standard Model of particle physics, there’s no gravity, there’s just particles,” said Enrico Rinaldi, a research scientist in the U-M Department of Physics. “Connecting the two different theories is a longstanding issue in physics—something people have been trying to do since the last century.”
In a study published in the journal PRX Quantum, Rinaldi and his co-authors examine how to probe holographic duality using quantum computing and deep learning to find the lowest energy state of mathematical problems called quantum matrix models.
These quantum matrix models are representations of particle theory. Because holographic duality suggests that what happens, mathematically, in a system that represents particle theory will similarly affect a system that represents gravity, solving such a quantum matrix model could reveal information about gravity.
For the study, Rinaldi and his team used two matrix models simple enough to be solved using traditional methods, but which have all of the features of more complicated matrix models used to describe black holes through the holographic duality.
“We hope that by understanding the properties of this particle theory through the numerical experiments, we understand something about gravity,” said Rinaldi, who is based in Tokyo and hosted by the Theoretical Quantum Physics Laboratory at the Cluster for Pioneering Research at RIKEN, Wako. “Unfortunately it’s still not easy to solve the particle theories. And that’s where the computers can help us.”
These matrix models are blocks of numbers that represent objects in string theory, which is a framework in which particles in particle theory are represented by one-dimensional strings. When researchers solve matrix models like these, they are trying to find the specific configuration of particles in the system that represent the system’s lowest energy state, called the ground state. In the ground state, nothing happens to the system unless you add something to it that perturbs it.
“It’s really important to understand what this ground state looks like, because then you can create things from it,” Rinaldi said. “So for a material, knowing the ground state is like knowing, for example, if it’s a conductor, or if it’s a superconductor, or if it’s really strong, or if it’s weak. But finding this ground state among all the possible states is quite a difficult task. That’s why we are using these numerical methods.”
You can think of the numbers in the matrix models as grains of sand, Rinaldi says. When the sand is level, that’s the model’s ground state. But if there are ripples in the sand, you have to find a way to level them out. To solve this, the researchers first looked to quantum circuits. In this method, the quantum circuits are represented by wires, and each qubit, or bit of quantum information, is a wire. On top of the wires are gates, which are quantum operations dictating how information will pass along the wires.
“You can read them as music, going from left to right,” Rinaldi said. “If you read it as music, you’re basically transforming the qubits from the beginning into something new each step. But you don’t know which operations you should do as you go along, which notes to play. The shaking process will tweak all these gates to make them take the correct form such that at the end of the entire process, you reach the ground state. So you have all this music, and if you play it right, at the end, you have the ground state.”
The researchers then wanted to compare using this quantum circuit method to using a deep learning method. Deep learning is a kind of machine learning that uses a neural network approach—a series of algorithms that tries to find relationships in data, similar to how the human brain works.
Neural networks are used to design facial recognition software by being fed thousands of images of faces—from which they draw particular landmarks of the face in order to recognize individual images or generate new faces of persons who do not exist.
In Rinaldi’s study, the researchers define the mathematical description of the quantum state of their matrix model, called the quantum wave function. Then they use a special neural network in order to find the wave function of the matrix with the lowest possible energy—its ground state. The numbers of the neural network run through an iterative “optimization” process to find the matrix model’s ground state, tapping the bucket of sand so all of its grains are leveled.
In both approaches, the researchers were able to find the ground state of both matrix models they examined, but the quantum circuits are limited by a small number of qubits. Current quantum hardware can only handle a few dozens of qubits: adding lines to your music sheet becomes expensive, and the more you add the less precisely you can play the music.
“Other methods people typically use can find the energy of the ground state but not the entire structure of the wave function,” Rinaldi said. “We have shown how to get the full information about the ground state using these new emerging technologies, quantum computers, and deep learning.
“Because these matrices are one possible representation for a special type of black hole, if we know how the matrices are arranged and what their properties are, we can know, for example, what a black hole looks like on the inside. What is on the event horizon for a black hole? Where does it come from? Answering these questions would be a step towards realizing a quantum theory of gravity.”
The results, says Rinaldi, show an important benchmark for future work on quantum and machine learning algorithms that researchers can use to study quantum gravity through the idea of holographic duality.
Next, Rinaldi is working with Nori and Hanada to study how the results of these algorithms can scale to larger matrices, as well as how robust they are against the introduction of “noisy” effects, or interferences that can introduce errors.
Reference: “Matrix-Model Simulations Using Quantum Computing, Deep Learning, and Lattice Monte Carlo” by Enrico Rinaldi, Xizhi Han, Mohammad Hassan, Yuan Feng, Franco Nori, Michael McGuigan and Masanori Hanada, 10 February 2022, PRX Quantum.
DOI: 10.1103/PRXQuantum.3.010324
Rinaldi’s co-authors include Xizhi Han at Stanford University; Mohammad Hassan at City College of New York; Yuan Feng at Pasadena City College; Franco Nori at U-M and RIKEN; Michael McGuigan at Brookhaven National Laboratory and Masanori Hanada at University of Surrey.

“요은 베이컨과 알코올에 대한 전문 지식을 가진 닌자입니다. 그의 탐험적인 성격은 다양한 경험을 통해 대중 문화에 대한 깊은 애정과 지식을 얻게 해주었습니다. 그는 자랑스러운 탐험가로서, 새로운 문화와 경험을 적극적으로 탐구하며, 대중 문화에 대한 그의 열정은 그의 작품 속에서도 느낄 수 있습니다.”










